Một trong những bài toán cơ bản liên quan đến mặt phẳng là viết phương trình mặt phẳng khi biết một điểm. Đây là nền tảng để giải quyết nhiều bài toán phức tạp hơn như xác định giao tuyến hai mặt phẳng, tìm khoảng cách từ điểm đến mặt phẳng, hay xét quan hệ song song, vuông góc giữa các đối tượng trong không gian.
Vậy làm thế nào để xác định được phương trình mặt phẳng khi chỉ biết một điểm? Cần thêm yếu tố gì để có thể viết được phương trình chính xác? Trong bài viết này, chúng ta sẽ cùng tìm hiểu lý thuyết quan trọng, các phương pháp giải bài toán và thực hành với những ví dụ từ cơ bản đến nâng cao.
1. Cách viết phương trình mặt phẳng khi biết một điểm
Muốn viết phương trình mặt phẳng trong dạng toán này ta cần trải qua 4 bước sau:
Bước 1: Xác định dữ kiện đề bài
- Gọi điểm đã cho là \( A(x_0, y_0, z_0) \).
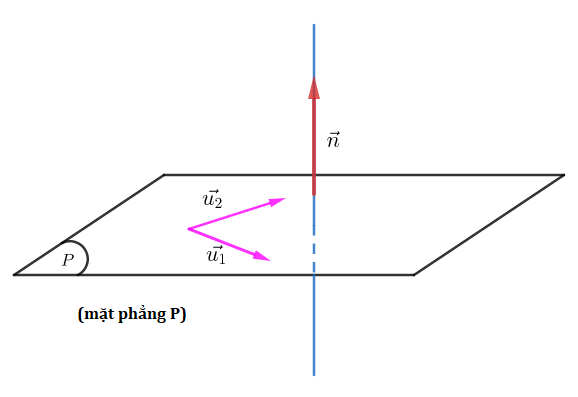
- Gọi vectơ pháp tuyến của mặt phẳng là \( \overrightarrow{n} = (a, b, c) \).
Bước 2: Viết phương trình tổng quát của mặt phẳng
Phương trình mặt phẳng đi qua điểm \( A(x_0, y_0, z_0) \) và có vectơ pháp tuyến \( (a, b, c) \) có dạng:
$ a(x – x_0) + b(y – y_0) + c(z – z_0) = 0 $
Bước 3: Thay số vào phương trình
- Thay \( (x_0, y_0, z_0) \) và \( (a, b, c) \) vào phương trình trên.
- Rút gọn để có phương trình mặt phẳng dưới dạng chuẩn.
Bước 4: Kiểm tra lại
- Xem phương trình có đúng với điểm đã cho không bằng cách thay tọa độ điểm vào phương trình.
- Đảm bảo hệ số của phương trình đã rút gọn hợp lý.
2. Bài tập vận dụng
Bài tập 1. Trong không gian \(Oxyz\), viết phương trình mặt phẳng \((P)\) đi qua điểm \(A(1;0;-2)\) và có vectơ pháp tuyến \(\vec{n}(1;-1;2)\).
Lời giải
Mặt phẳng \((P)\) đi qua điểm \(A(1;0;-2)\) và có vectơ pháp tuyến \(\vec{n}(1;-1;2)\) có phương trình là:
$ 1(x – 1) – 1(y – 0) + 2(z + 2) = 0 $ $ \Leftrightarrow x – y + 2z + 3 = 0 $
Vậy phương trình mặt phẳng \((P)\) là: $ x – y + 2z + 3 = 0. $
Bài tập 2. Trong không gian với hệ trục tọa độ \( Oxyz \), viết phương trình mặt phẳng đi qua điểm \( A(0;1;2) \) và có vectơ pháp tuyến \( \overrightarrow{n} = (-2;1;0) \).
Lời giải
Vậy phương trình mặt phẳng đi qua điểm \( A(0;1;2) \) và có vectơ pháp tuyến \( \overrightarrow{n} = (-2;1;0) \) có dạng:
$ -2(x – 0) + 1(y – 1) = 0 $ $ \Leftrightarrow -2x + y – 1 = 0 $ $ \Leftrightarrow 2x – y + 1 = 0. $
Bạn cần chỉnh sửa hay bổ sung gì không?
Bài tập 3. Trong không gian \( Oxyz \), viết phương trình mặt phẳng đi qua \( A(-1;1;1) \) và có vectơ pháp tuyến \( \overrightarrow{n} = (-1;-2;2) \).
Lời giải
Mặt phẳng đi qua \( A(-1;1;1) \), có vectơ pháp tuyến \( \overrightarrow{n} ( -1; -2; 2 ) \), suy ra phương trình mặt phẳng cần tìm là
$ -1(x + 1) – 2(y – 1) + 2(z – 1) = 0 $ $ \Leftrightarrow -x – 2y + 2z – 1 = 0. $
Bài tập 4. Trong không gian với hệ tọa độ \( Oxyz \), cho hai điểm \( A(1;6;-7) \) và \( B(3;2;1) \). Phương trình mặt phẳng trung trực đoạn \( AB \) là.
Lời giải
Mặt phẳng trung trực đoạn \( AB \) đi qua trung điểm \( I(2;4;-3) \) của đoạn \( AB \) và nhận \( \overrightarrow{AB} = (2;-4;8) \) làm vectơ pháp tuyến có phương trình:
$ 2(x – 2) – 4(y – 4) + 8(z + 3) = 0 $ $ \Leftrightarrow x – 2y + 4z + 18 = 0. $
Bài tập 5. Trong không gian \( Oxyz \), cho \( A(-1;-1;1) \), \( B(3;1;1) \). Phương trình mặt phẳng trung trực của đoạn \( AB \) là.
Lời giải
Gọi \( I \) là trung điểm của \( AB \) nên \( I(1;0;1) \).
Mặt phẳng trung trực của đoạn \( AB \) có vectơ pháp tuyến là $\overrightarrow{n} = \overrightarrow{AB} = (4;2;0) = 2(2;1;0).$
Phương trình mặt phẳng cần tìm là: $ 2(x – 1) + 1(y – 0) = 0 $ $ \Leftrightarrow 2x + y – 2 = 0. $
Bài tập 6. Trong không gian với hệ trục tọa độ \( Oxyz \), cho các điểm \( A(0;1;2) \), \( B(2;-2;1) \), \( C(-2;0;1) \). Phương trình mặt phẳng đi qua \( A \) và vuông góc với \( BC \) là?
Lời giải
Ta có: \( \overrightarrow{n} = \overrightarrow{BC} = (-2;1;0) \).
Vậy phương trình mặt phẳng đi qua \( A \) và vuông góc với \( BC \) có dạng: $ -2(x – 0) + 1(y – 1) = 0 $ $ \Leftrightarrow -2x + y – 1 = 0 $ $ \Leftrightarrow 2x – y + 1 = 0. $
