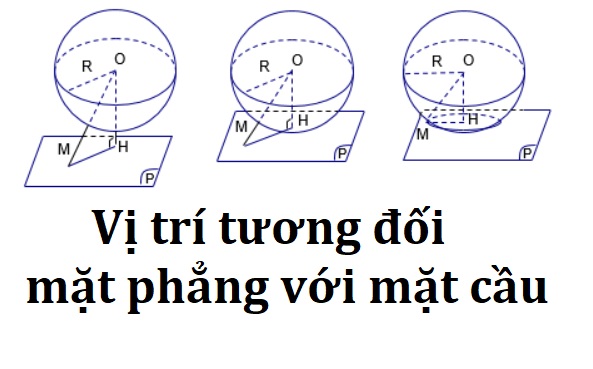
Trong hình học không gian, vị trí tương đối mặt phẳng với mặt cầu là dạng toán quan trọng, thường gặp trong đề thi THPT. Bài toán này giúp xác định khi nào mặt phẳng cắt, tiếp xúc hoặc không cắt mặt cầu, đồng thời tính bán kính giao tuyến nếu có. Để giải dạng toán này, học sinh cần nắm vững công thức khoảng cách từ tâm cầu đến mặt phẳng và hệ thức liên quan. Việc luyện tập thường xuyên qua các bài tập minh họa sẽ giúp học sinh làm chủ phương pháp, nâng cao kỹ năng giải bài tập hình học không gian nhanh và chính xác.
1. Vị trí tương đối giữa mặt phẳng (P) và mặt cầu (S)
Cho mặt cầu S(I; R) và mặt phẳng (P).
Gọi H là hình chiếu vuông góc của I lên (P) và có \( d = IH \) là khoảng cách từ I đến mặt phẳng (P).
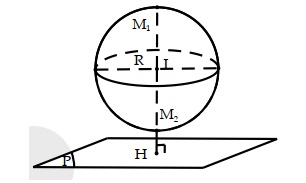
Khi đó:
- Nếu \( d > R \): Mặt cầu và mặt phẳng không có điểm chung.
- Nếu \( d = R \): Mặt phẳng tiếp xúc mặt cầu.
Khi (P) là mặt phẳng tiếp diện của (S) và H là tiếp điểm.
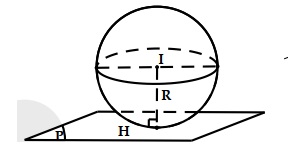
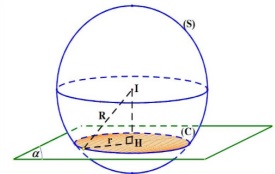
- Nếu \( d < R \): mặt phẳng (P) cắt mặt cầu theo thiết diện là đường tròn có tâm H và bán kính \( r = \sqrt{R^2 – IH^2} \).
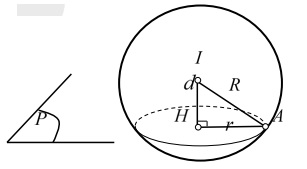
Viết phương trình mặt (P) // (Q): ax + by + cz + d = 0 và tiếp xúc với mặt cầu (S).
Phương pháp:
- Vì (P)// (Q): ax + by + cz + d = 0 ⇒ (P) : ax + by + cz + d’ = 0.
- Tìm tâm I và bán kính R của mặt cầu.
- Vì (P) tiếp xúc (S) nên có \( d{I;(P)} = R \Rightarrow d’ \).
2. Bài tập vận dụng
Bài tập 1. (Thpt Vĩnh Lộc – Thanh Hóa 2019) Cho mặt cầu \( (S) \) có phương trình $ (x – 3)^2 + (y + 2)^2 + (z – 1)^2 = 100 $ và mặt phẳng \( (\alpha) \) có phương trình $ 2x – 2y – z + 9 = 0. $ Tính bán kính của đường tròn \( (C) \) là giao tuyến của mặt phẳng \( (\alpha) \) và mặt cầu \( (S) \).
A. 8.
B. \( 4\sqrt{6} \).
C. 10.
D. 6.
Chọn A
Lời giải
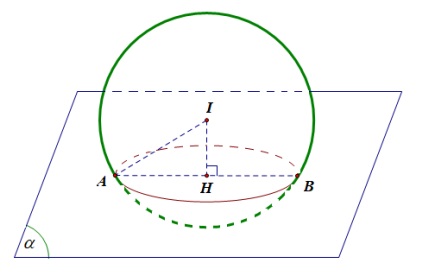
Gọi \( I \) là tâm mặt cầu \( (S) \), \( H \) là hình chiếu vuông góc của \( I \) lên mặt phẳng \( (\alpha) \) và \( AB \) là một đường kính của đường tròn \( (C) \).
Dễ thấy \( I(3;-2;1) \), \( IA = 10 \), \( IH = d(I,(\alpha)) = 6 \)
suy ra $HA = \sqrt{IA^2 – IH^2} = 8.$
Vậy bán kính đường tròn \( (C) \) bằng 8.
Bài tập 2. (SGD Bến Tre 2019) Trong không gian \( Oxyz \) cho mặt cầu \( (S) \): $ x^2 + y^2 + z^2 – 2x – 4y – 6z = 0. $ Đường tròn giao tuyến của \( (S) \) với mặt phẳng \( (Oxy) \) có bán kính là
A. \( r = 3 \).
B. \( r = \sqrt{5} \).
C. \( r = \sqrt{6} \).
D. \( r = \sqrt{14} \).
Lời giải
Mặt cầu \( (S) \) có tâm \( I(1;2;3) \) và bán kính
$R = \sqrt{1^2 + 2^2 + 3^2} = \sqrt{14}.$
Khoảng cách từ tâm \( I \) đến mặt phẳng \( (Oxy) \) là \( d = 3 \), suy ra bán kính đường tròn giao tuyến cần tìm là
$r = \sqrt{R^2 – d^2} = \sqrt{5}.$
Bài tập 3. Trong không gian \( Oxyz \), cho mặt cầu \( (S) \): $ (x – 2)^2 + (y – 4)^2 + (z – 1)^2 = 4 $ và mặt phẳng \( (P) \): $ x + my + z – 3m – 1 = 0. $
Tìm tất cả các giá trị thực của tham số \( m \) để mặt phẳng \( (P) \) cắt mặt cầu \( (S) \) theo giao tuyến là đường tròn có đường kính bằng 2.
A. \( m = 1 \).
B. \( m = -1 \) hoặc \( m = -2 \).
C. \( m = 1 \) hoặc \( m = 2 \).
D. \( m = -1 \).
Lời giải
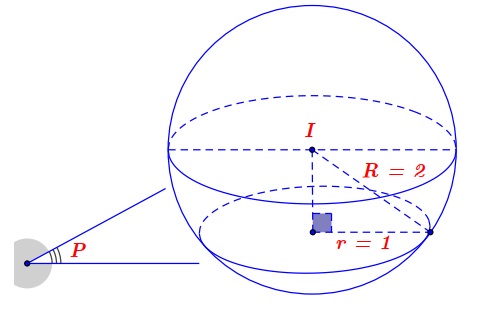
Mặt cầu \( (S) \): $ (x – 2)^2 + (y – 4)^2 + (z – 1)^2 = 4 $ có tâm \( I(2;4;1) \), bán kính \( R = 2 \).
Ta có $ d(I, (P)) = \frac{|2 + 4m + 1 – 3m – 1|}{\sqrt{1 + m^2 + 1}} = \frac{|m + 2|}{\sqrt{m^2 + 2}}. $
Mặt phẳng \( (P) \) cắt mặt cầu \( (S) \) theo giao tuyến là đường tròn có đường kính bằng 2 nên bán kính đường tròn giao tuyến \( r = 1 \).
Ta có $ R^2 = d^2 (I, (P)) + r^2 $ $ 4 = \frac{(m + 2)^2}{m^2 + 2} + 1 \Leftrightarrow m^2 + 4m + 4 = 3(m^2 + 2) \Leftrightarrow 2m^2 – 4m + 2 = 0 $ $ \Leftrightarrow m = 1. $
Bài tập 4. (SGD Bình Phước – 2019) Trong không gian \( Oxyz \), cho mặt phẳng \( (P) : x + 2y – 2z + 3 = 0 \) và mặt cầu \( (S) \) có tâm \( I(0;-2;1) \). Biết mặt phẳng \( (P) \) cắt mặt cầu \( (S) \) theo giao tuyến là một đường tròn có diện tích \( 2\pi \). Mặt cầu \( (S) \) có phương trình là
A. \( x^2 + (y + 2)^2 + (z + 1)^2 = 2. \)
B. \( x^2 + (y + 2)^2 + (z – 1)^2 = 3. \)
C. \( x^2 + (y + 2)^2 + (z + 1)^2 = 3. \)
D. \( x^2 + (y + 2)^2 + (z + 1)^2 = 1. \)
Lời giải
Chọn B
Gọi \( R, r \) lần lượt là bán kính của mặt cầu và đường tròn giao tuyến.
Theo giả thiết ta có: $ \pi r^2 = 2\pi \Leftrightarrow r^2 = 2 $ Mặt khác \( d(I,(P))=1 \) nên $ R^2 = r^2 + \left[ d(I,(P)) \right]^2 = 3. $
Vậy phương trình mặt cầu là \( x^2 + (y + 2)^2 + (z – 1)^2 = 3 \).
Bài tập 5. (THPT Ba Đình – 2019) Trong không gian với hệ trục tọa độ \( Oxyz \), cho mặt phẳng $ (P): mx + 2y – z + 1 = 0 \quad (m \text{ là tham số}). $ Mặt phẳng \( (P) \) cắt mặt cầu $ (S): (x – 2)^2 + (y – 1)^2 + z^2 = 9 $ theo một đường tròn có bán kính bằng 2. Tìm tất cả các giá trị thực của tham số \( m \)?
A. \( m = \pm 1 \).
B. \( m = \pm 2 + \sqrt{5} \).
C. \( m = \pm 4 \).
D. \( m = 6 \pm 2\sqrt{5} \).
Lời giải
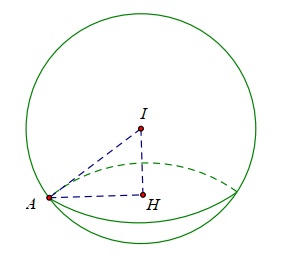
Từ \( (S): (x – 2)^2 + (y – 1)^2 + z^2 = 9 \) ta có tâm \( I = (2;1;0) \) bán kính \( R = 3 \). Gọi \( H \) là hình chiếu vuông góc của \( I \) trên \( (P) \) và
$(P) \cap (S) = C(H;r) \quad \text{với } r = 2$
Ta có \( IH = d \left( I; (P) \right) \) \( \Leftrightarrow \)
$IH = \dfrac{|2m + 2 – 0 + 1|}{\sqrt{m^2 + 4 + 1}} = \dfrac{|2m + 3|}{\sqrt{m^2 + 5}}$
Theo yêu cầu bài toán ta có \( R^2 = IH^2 + r^2 \) \( \Leftrightarrow \)
$9 = \dfrac{(2m + 3)^2}{m^2 + 5} + 4$
$ \Leftrightarrow {m^2} – 12m + 16 = 0 \Leftrightarrow \left[ {\begin{array}{{20}{l}} {m = 6 – 2\sqrt 5 }\\ {m = 6 + 2\sqrt 5 } \end{array}} \right.$
Bài tập 6. (Chuyên Quốc Học Huế – 2019) Trong không gian với hệ trục tọa độ \( Oxyz \) cho mặt phẳng \( (\alpha) \) có phương trình \( 2x + y – z – 1 = 0 \) và mặt cầu \( (S) \) có phương trình $(x – 1)^2 + (y – 1)^2 + (z + 2)^2 = 4.$
Xác định bán kính \( r \) của đường tròn là giao tuyến của mặt phẳng \( (\alpha) \) và mặt cầu \( (S) \).
A. \( r = \dfrac{2\sqrt{42}}{3}. \)
B. \( r = \dfrac{2\sqrt{3}}{3}. \)
C. \( r = \dfrac{2\sqrt{15}}{3}. \)
D. \( r = \dfrac{2\sqrt{7}}{3}. \)
Lời giải
Chọn B
Mặt cầu \( (S) \) có tâm \( I(1;1;-2) \) và bán kính \( R = 2 \). Gọi \( d \) là khoảng cách từ tâm \( I \) đến mặt phẳng \( (\alpha) \). Ta có $ d = d(I,(\alpha)) = \dfrac{2\sqrt{6}}{3}. $
Khi đó ta có: $ r = \sqrt{R^2 – d^2} = \dfrac{2\sqrt{3}}{3}. $