Trong hình học không gian, vecto pháp tuyến của mặt phẳng đóng vai trò quan trọng trong việc xác định phương và vị trí của một mặt phẳng. Đây không chỉ là kiến thức nền tảng trong toán học mà còn có nhiều ứng dụng thực tế, từ giải bài tập hình học đến các lĩnh vực như kỹ thuật. Để nắm vững chủ đề này, việc hiểu rõ lý thuyết kết hợp với luyện tập qua các bài tập từ cơ bản đến nâng cao là vô cùng cần thiết. Trong bài viết này, chúng ta sẽ cùng khám phá cách xác định vecto pháp tuyến mặt phẳng một cách dễ hiểu, đồng thời áp dụng vào các dạng bài tập phổ biến để củng cố kiến thức.
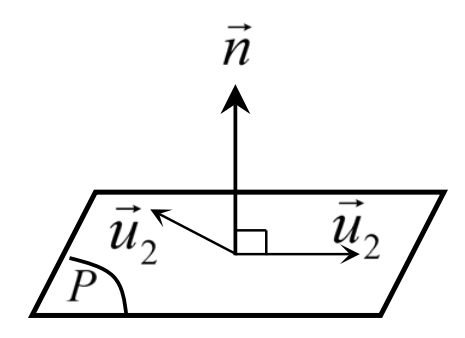
1. Cách xác định vecto pháp tuyến của mặt phẳng
Để tìm vecto pháp tuyến mặt phẳng, ta cần làm 3 bước sau:
Bước 1: Xác định phương trình mặt phẳng
Mặt phẳng thường được cho dưới các dạng:
- Dạng tổng quát: \( ax + by + cz + d = 0 \)
- Dạng tham số: Có hai véc tơ chỉ phương
- Dạng khác: Phương trình mặt phẳng theo đoạn chắn, phương trình tổng quát suy ra từ dạng khác
Bước 2: Xác định véc tơ pháp tuyến
- Nếu phương trình mặt phẳng có dạng tổng quát \( ax + by + cz + d = 0 \), thì véc tơ pháp tuyến của mặt phẳng là: $ \vec{n} = (a; b; c) $
- Nếu mặt phẳng được cho bằng hai véc tơ chỉ phương \( \vec{u_1}, \vec{u_2} \), thì véc tơ pháp tuyến được tìm bằng tích có hướng: $ \vec{n} = \vec{u_1} \times \vec{u_2} $
- Nếu phương trình mặt phẳng ở dạng khác, cần biến đổi về dạng tổng quát rồi lấy hệ số \( x, y, z \) làm tọa độ véc tơ pháp tuyến.
Bước 3: Kiểm tra kết quả
- Xem xét véc tơ tìm được có phù hợp với phương trình mặt phẳng hay không.
- Nếu đề bài yêu cầu chọn đáp án tương đương, cần kiểm tra các véc tơ cùng phương (tỉ lệ với véc tơ pháp tuyến ban đầu).
Nhận xét
- Một mặt phẳng có vô số véc tơ pháp tuyến cùng phương nhau.
- Nếu véc tơ \( \vec{n} \) là một véc tơ pháp tuyến thì mọi véc tơ \( k\vec{n} \) (với \( k \neq 0 \)) cũng là véc tơ pháp tuyến.
- Khi phương trình mặt phẳng có dạng đặc biệt, cần khéo léo biến đổi để xác định véc tơ pháp tuyến.
2. Bài tập
Bài tập 1: Trong không gian \( Oxyz \), vectơ nào dưới đây là một vectơ pháp tuyến của mặt phẳng \( (P) : 2y – 3z + 1 = 0 \)?
Lời giải
Ta có \( \vec{u_2} = (0;2;-3) \) là một vectơ pháp tuyến của mặt phẳng \( (P) : 2y – 3z + 1 = 0 \).
Bài tập 2. Trong không gian \( Oxyz \), một vectơ pháp tuyến của mặt phẳng \( \frac{x}{-2} + \frac{y}{-1} + \frac{z}{3} = 1 \) là
A. \( \vec{n} = (3;6;-2) \).
B. \( \vec{n} = (2;-1;3) \).
C. \( \vec{n} = (-3;-6;-2) \).
D. \( \vec{n} = (-2;-1;3) \).
Lời giải
Phương trình \( \frac{x}{-2} + \frac{y}{-1} + \frac{z}{3} = 1 \)
\( \Leftrightarrow -\frac{1}{2} x – y + \frac{1}{3} z – 1 = 0 \).
\( \Leftrightarrow 3x + 6y – 2z + 6 = 0 \).
Một vectơ pháp tuyến của mặt phẳng \( \vec{n} = (3;6;-2) \).
Bài tập 3. Cho mặt phẳng \( (P) : 3x – y + 2 = 0 \). Véc tơ nào trong các véc tơ dưới đây là một véc tơ pháp tuyến của mặt phẳng \( (P) \)?
A. \( (3;-1;2) \).
B. \( (-1;0;-1) \).
C. \( (3;0;-1) \).
D. \( (3;-1;0) \).
Lời giải
Một vectơ pháp tuyến của mặt phẳng \( (P) : 3x – y + 2 = 0 \) là \( (3;-1;0) \).
Bài tập 4. Cho mặt phẳng \( (\alpha) : 2x – 3y – 4z + 1 = 0 \). Khi đó, một véc tơ pháp tuyến của \( (\alpha) \)
A. \( \vec{n} = (2;3;-4) \).
B. \( \vec{n} = (2;-3;4) \).
C. \( \vec{n} = (-2;3;4) \).
D. \( \vec{n} = (-2;3;1) \).
Lời giải
📌 Chọn C
Mặt phẳng \( (\alpha) : 2x – 3y – 4z + 1 = 0 \) có một véc tơ pháp tuyến \( \vec{n_0} = (2;-3;-4) \).
Nhận thấy \( \vec{n} = (-2;3;4) = -\vec{n_0} \), hay \( \vec{n} \) cùng phương với \( \vec{n_0} \).
Do đó véc tơ \( \vec{n} = (-2;3;4) \) cũng là một véc tơ pháp tuyến của mặt phẳng \( (\alpha) \).
Bài tập 5. Trong mặt phẳng tọa độ \( Oxyz \), cho phương trình tổng quát của mặt phẳng \( (P) : 2x – 6y – 8z + 1 = 0 \). Một véc tơ pháp tuyến của mặt phẳng \( (P) \) có tọa độ là:
A. \( (-1;-3;4) \)
B. \( (1;3;4) \)
C. \( (1;-3;-4) \)
D. \( (1;-3;4) \)
Lời giải
Phương trình tổng quát của mặt phẳng \( (P) : 2x – 6y – 8z + 1 = 0 \) nên một véc tơ pháp tuyến của mặt phẳng \( (P) \) có tọa độ là \( (2;-6;-8) \) hay \( (1;-3;-4) \).