Công thức tính diện tích xung quanh hình nón cụt

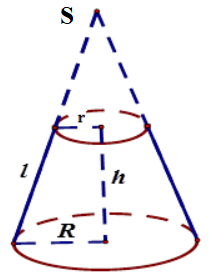
Như đã tìm hiểu từ bài công thức Toán hình lớp 9, Hình nón cụt là phần của một hình nón bị cắt ngang bởi một mặt phẳng song song với đáy của nó. Kết quả tạo ra một hình khối có hai đáy là hai hình tròn song song và một mặt xung quanh cong nối hai đáy. Nếu mặt cắt không song song với đáy thì phần còn lại không phải là hình nón cụt mà là một hình không gian khác.

1. Tính diện tích xung quanh của hình nón cụt

Diện tích xung quanh của hình nón cụt được tính bằng:

${S_{xq}} = \pi .\ell .\left( {R + r} \right)$

Trong đó:

• ℓ: đường sinh của hình nón cụt.
• R: bán kính đáy lớn.
• r: bán kính đáy nhỏ.
• π là hằng số (≈ 3.14).

⇒Muốn tính được đường sinh ℓ bằng định lý Pythagoras nếu chưa có: $\ell = \sqrt {{h^2} + {{\left( {R – r} \right)}^2}} $, với h là chiều cao của hình nón cụt.

⇒ Thay giá trị vào công thức để tính diện tích xung quanh.

2. Tính diện tích toàn phần của hình nón cụt

Diện tích toàn phần của hình nón cụt bao gồm diện tích xung quanh và diện tích hai đáy:

S_tp = S_xq + S_{đáy lớn} + S_{đáy nhỏ}

Trong đó:

• S_{đáy lớn} = π × R²
• S_{đáy nhỏ} = π × r²

⇒ Tính diện tích xung quanh Sxq bằng công thức trên.

⇒ Tính diện tích hai đáy.

⇒ Cộng tất cả lại để ra diện tích toàn phần.

3. Tính thể tích của hình nón cụt

Thể tích hình nón cụt được tính bằng:

$V = \frac{1}{3}.\pi .h.\left( {{R^2} + R + r + {r^2}} \right)$

Trong đó:

• h: chiều cao của hình nón cụt.
• R: bán kính đáy lớn.
• r: bán kính đáy nhỏ.

⇒ Xác định các giá trị cần thiết (chiều cao h, bán kính R, r).

⇒ Thay vào công thức để tính thể tích.

4. Tìm các yếu tố khác (chiều cao, đường sinh, bán kính,…)

Những dạng bài tập thường gặp

• Tìm chiều cao: Sử dụng định lý Pythagoras: $h = \sqrt {{\ell ^2} – {{\left( {R – r} \right)}^2}} $
• Tìm đường sinh: $\ell = \sqrt {{h^2} + {{\left( {R – r} \right)}^2}} $
• Tìm bán kính đáy lớn hoặc nhỏ: Sử dụng các công thức đã học để giải ngược.

5. Bài tập minh họa

Bài tập 1: Cho hình nón cụt có bán kính đáy lớn R = 6 cm, bán kính đáy nhỏ r = 4 cm, và chiều cao h = 8 cm. Tính diện tích xung quanh.

Lời giải

Tính đường sinh ℓ:

$\ell = \sqrt {{h^2} + {{\left( {R – r} \right)}^2}} $

$ = \sqrt {{8^2} + {{\left( {6 – 4} \right)}^2}} $

$ = 8,25\left( {cm} \right)$

Tính diện tích xung quanh:

S_xq = π × ℓ × (R + r)

= 3.14 × 8.25 × (6 + 4) = 259.05 cm².

Bài tập 2: Cho hình nón cụt có bán kính đáy lớn R = 5 cm, bán kính đáy nhỏ r = 3 cm, và chiều cao h = 9 cm. Tính thể tích.

Lời giải

Thay vào công thức thể tích:

$V = \frac{1}{3}.\pi .h.\left( {{R^2} + R + r + {r^2}} \right)$

Thay số: $V = \frac{1}{3}.\pi .9.\left( {{5^2} + 5 + 3 + {3^3}} \right)$ = $461,58\left( {c{m^3}} \right)$

Hình nón cụt là một khối hình học không gian quan trọng cả trong lý thuyết và thực tiễn. Việc nắm vững các công thức và tính chất của hình nón cụt giúp chúng ta có thể ứng dụng vào nhiều lĩnh vực khác nhau, từ học thuật đến sản xuất và đời sống hàng ngày.