Phương trình mặt phẳng là kiến thức quan trọng trong hình học Oxyz, thường xuất hiện trong các bài kiểm tra và kỳ thi quan trọng. Việc nắm vững công thức và cách giải giúp bạn tự tin xử lý các bài toán từ cơ bản đến nâng cao. Trong bài viết này, chúng ta sẽ đi sâu vào lý thuyết, các dạng bài tập phương trình mặt phẳng kèm lời giải chi tiết, giúp bạn luyện tập hiệu quả và đạt điểm cao. Nếu bạn đang tìm kiếm tài liệu học tập đầy đủ và dễ hiểu, đây chính là hướng dẫn dành cho bạn!
1. Cách viết phương trình mặt phẳng
Mặt phẳng \( (P) \) qua \( M(x_0; y_0; z_0) \) và có vecto pháp tuyến $\vec n = (a;b;c)$
thì phương trình \( (P) \): $a(x – x_0) + b(y – y_0) + c(z – z_0) = 0$
Ngược lại, một mặt phẳng bất kỳ đều có phương trình dạng \( ax + by + cz + d = 0 \), mặt phẳng này có \(\overrightarrow{VTPT} \quad \overrightarrow{n} = (a; b; c)\) với \( a^2 + b^2 + c^2 > 0 \).
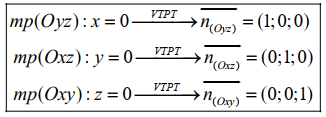
Các mặt phẳng cơ bản
Viết phương trình mặt phẳng qua \( M \) và vuông góc với đường thẳng \( AB \) cho trước.
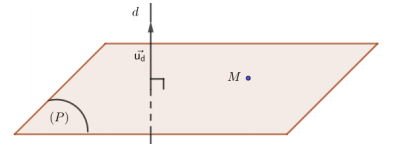
Mặt phẳng qua \( M \), có vecto pháp tuyến ${\vec n_{(P)}} = \overrightarrow {AB} $ nên phương trình được viết theo.
2. Bài tập vận dụng
Bài tập 1. Trong không gian \( Oxyz \), phương trình mặt phẳng đi qua ba điểm \( A(1;0;0) \), \( B(0;-2;0) \) và \( C(0;0;3) \) là
A. \( \frac{x}{1} + \frac{y}{-2} + \frac{z}{3} = 1 \).
B. \( \frac{x}{1} + \frac{y}{-2} + \frac{z}{3} = -1 \).
C. \( \frac{x}{1} + \frac{y}{-2} + \frac{z}{3} = 0 \).
D. \( \frac{x}{1} + \frac{y}{2} + \frac{z}{3} = 1 \).
Lời giải
Ta có phương trình mặt phẳng đi qua ba điểm \( A(1;0;0) \), \( B(0;-2;0) \) và \( C(0;0;3) \) là:
$\frac{x}{1} + \frac{y}{-2} + \frac{z}{3} = 1.$
Bài tập 2. Cho ba điểm \( A(2;1;-1) \), \( B(-1;0;4) \), \( C(0;-2;-1) \). Phương trình mặt phẳng đi qua \( A \) và vuông góc với \( BC \) là
A. \( x – 2y – 5z – 5 = 0 \).
B. \( 2x – y + 5z – 5 = 0 \).
C. \( x – 2y – 5 = 0 \).
D. \( x – 2y – 5z + 5 = 0 \).
Lời giải
Do mặt phẳng vuông góc với \( BC \) nên \( \overrightarrow{BC} = (1;-2;-5) \) là vectơ pháp tuyến của mặt phẳng.
Vì vậy phương trình mặt phẳng là: \( 1(x – 2) -2(y -1) -5(z +1) = 0 \Leftrightarrow x – 2y – 5z – 5 = 0 \).
Bài tập 3. Trong không gian \( Oxyz \) phương trình mặt phẳng đi qua điểm \( A(1;-2;3) \) và vuông góc với giá của vectơ \( \overrightarrow{v} = (-1;2;3) \) là
A. \( x – 2y – 3z – 4 = 0 \).
B. \( -x + 2y + 3z – 4 = 0 \).
C. \( x – 2y – 3z + 4 = 0 \).
D. \( -x + 2y – 3z + 4 = 0 \).
Lời giải
📌 Chọn C
Phương trình mặt phẳng đi qua điểm \( A(1;-2;3) \) và vuông góc với giá của vectơ \( \overrightarrow{v} = (-1;2;3) \) là:
$-1(x – 1) + 2(y + 2) + 3(z – 3) = 0 \Leftrightarrow -x + 2y + 3z – 4 = 0 \Leftrightarrow x – 2y – 3z + 4 = 0.$
Bài tập 4. Trong không gian \( Oxyz \), cho 2 điểm \( A(5;-4;2) \) và \( B(1;2;4) \). Mặt phẳng đi qua \( A \) và vuông góc với đường thẳng \( AB \) là?
A. \( 3x – y + 3z – 25 = 0 \)
B. \( 2x – 3y – z + 8 = 0 \)
C. \( 3x – y + 3z – 13 = 0 \)
D. \( 2x – 3y – z – 20 = 0 \)
Lời giải
Chọn D
Mặt phẳng vuông góc với đường thẳng \( AB \) nên nhận \( \overrightarrow{AB} \) làm vectơ pháp tuyến,
\( \overrightarrow{AB} = (-4;6;2) \)
Mặt phẳng đi qua \( A(5;-4;2) \) và có vectơ pháp tuyến, \( \overrightarrow{AB} = (-4;6;2) \) có phương trình
\(-4(x – 5) + 6(y + 4) + 2(z – 2) = 0\) hay \( 2x – 3y – z – 20 = 0 \). Vậy Chọn D
Bài tập 5. Trong không gian với hệ trục tọa độ \( Oxyz \), phương trình mặt phẳng đi qua điểm \( A(1;2;-3) \) có vectơ pháp tuyến \( \overrightarrow{n} = (2;-1;3) \) là
A. \( 2x – y + 3z + 9 = 0 \).
B. \( 2x – y + 3z – 4 = 0 \).
C. \( x – 2y – 4 = 0 \).
D. \( 2x – y + 3z + 4 = 0 \).
Lời giải
📌 Chọn A
Phương trình mặt phẳng đi qua điểm \( A(1;2;-3) \) có vectơ pháp tuyến \( \overrightarrow{n} = (2;-1;3) \) là $ 2(x – 1) – 1(y – 2) + 3(z + 3) = 0 $
$ \Leftrightarrow 2x – 2 – y + 2 + 3z + 9 = 0 $ $ \Leftrightarrow 2x – y + 3z + 9 = 0. $
Bài tập 6. Trong không gian với hệ tọa độ \( Oxyz \), phương trình nào sau đây là phương trình của mặt phẳng \( Ozx \)?
A. \( x = 0 \).
B. \( y – 1 = 0 \).
C. \( y = 0 \).
D. \( z = 0 \).
Lời giải
Ta có mặt phẳng \( Ozx \) đi qua điểm \( O(0;0;0) \) và vuông góc với trục \( Oy \) nên có VTPT \( \overrightarrow{n} = (0;1;0) \).
Bài tập 7. Trong không gian \( Oxyz \), cho hai điểm \( A(1;2;0) \) và \( B(2;3;-1) \). Phương trình mặt phẳng qua \( A \) và vuông góc với \( AB \) là
A. \( 2x + y – z – 3 = 0 \).
B. \( x + y – z + 3 = 0 \).
C. \( x + y – z – 3 = 0 \).
D. \( x – y – z – 3 = 0 \).
Lời giải
📌 Chọn C
➤ \( \overrightarrow{AB} (1;1;-1) \).
➤ Mặt phẳng qua \( A \) và vuông góc với \( AB \) nhận \( \overrightarrow{AB} \) làm vectơ pháp tuyến có phương trình là $ x – 1 + y – 2 – z = 0 \Leftrightarrow x + y – z – 3 = 0. $
Bài tập 8. Trong không gian \( Oxyz \), mặt phẳng \( (P) \) đi qua điểm \( M(3;-1;4) \) đồng thời vuông góc với giá của vectơ \( \overrightarrow{a} = (1;-1;2) \) có phương trình là
A. \( 3x – y + 4z – 12 = 0 \).
B. \( 3x – y + 4z + 12 = 0 \).
C. \( x – y + 2z – 12 = 0 \).
D. \( x – y + 2z + 12 = 0 \).
Lời giải
📌 Chọn C
Mặt phẳng \( (P) \) đi qua điểm \( M(3;-1;4) \) đồng thời vuông góc với giá của \( \overrightarrow{a} = (1;-1;2) \) nên nhận \( \overrightarrow{a} = (1;-1;2) \) làm vectơ pháp tuyến. Do đó, \( (P) \) có phương trình là
$1(x – 3) – 1(y + 1) + 2(z – 4) = 0 \Leftrightarrow x – y + 2z – 12 = 0.$
Vậy, ta chọn C.
Bài tập 9. Trong không gian \( Oxyz \), cho hai điểm \( A(1;1;2) \) và \( B(2;0;1) \). Mặt phẳng đi qua \( A \) và vuông góc với \( AB \) có phương trình là
A. \( x + y – z = 0 \).
B. \( x – y – z – 2 = 0 \).
C. \( x + y + z – 4 = 0 \).
D. \( x – y – z + 2 = 0 \).
Lời giải
Ta có: \( \overrightarrow{AB} = (1;-1;-1) \).
Phương trình mặt phẳng đi qua \( A \) và vuông góc với \( AB \) có phương trình là: $ (x – 1) – (y – 1) – (z – 2) = 0 \Leftrightarrow x – y – z + 2 = 0. $
Bài tập 10. Trong không gian \( Oxyz \), mặt phẳng \( (Oxy) \) có phương trình là
A. \( z = 0 \).
B. \( x = 0 \).
C. \( y = 0 \).
D. \( x + y = 0 \).
Lời giải
Chọn A
Mặt phẳng \( (Oxy) \) đi qua gốc tọa độ \( O(0;0;0) \), nhận vectơ đơn vị \( \overrightarrow{k} = (0;0;1) \) là vectơ pháp tuyến
\(\Rightarrow\) Phương trình tổng quát: \( 0.(x-0) + 0.(y-0) + 1.(z-0) = 0 \Rightarrow (Oxy) : z = 0 \).
Bài tập 11. Trong không gian \( Oxyz \), mặt phẳng \( (P) \) đi qua điểm \( M(3;-1;4) \) đồng thời vuông góc với giá của vectơ \( \overrightarrow{a} = (1;-1;2) \) có phương trình là
A. \( 3x – y + 4z – 12 = 0 \).
B. \( 3x – y + 4z + 12 = 0 \).
C. \( x – y + 2z – 12 = 0 \).
D. \( x – y + 2z + 12 = 0 \).
Lời giải
Chọn C
\( (P) \) có dạng: \( 1.(x – 3) -1(y +1) + 2(z – 4) = 0 \Leftrightarrow x – y + 2z – 12 = 0 \).
