Hình nón là gì? Công thức tính diện tích xung quanh hình nón và thể tích hình nón

Hình nón là một hình quan trọng trọng trong hình học không gian ba chiều, thường được nghiên cứu trong các bài toán về diện tích, thể tích, và các bài toán liên quan đến mối quan hệ giữa các yếu tố của hình nón (bán kính, chiều cao, đường sinh).

Ở bài công thức Toán hình lớp 9, HinhHoc đã giới thiếu sơ lược về các công thức thường gặp ở hình nón. Dưới đây là các dạng bài tập phổ biến về hình nón cùng với công thức áp dụng:

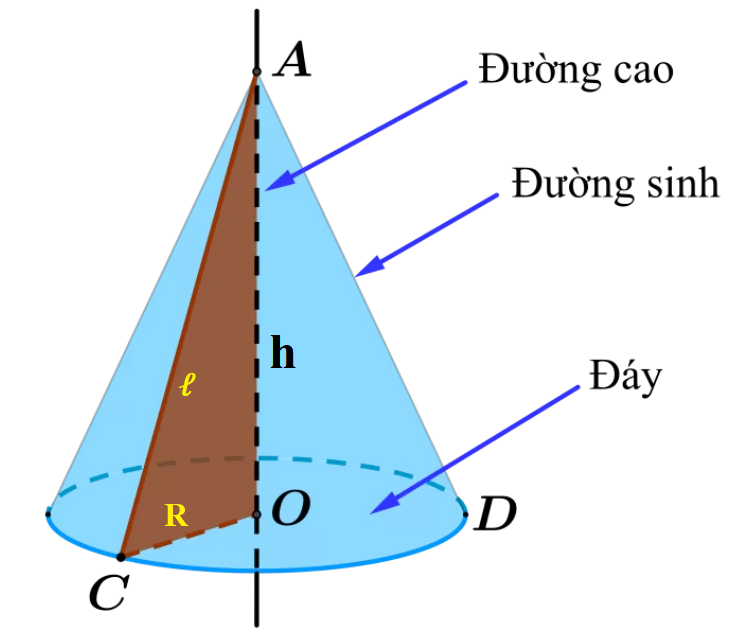
1. Tính diện tích xung quanh của hình nón

 Công thức: $ S_{\text{xq}} = \pi r l $

Trong đó:

• \( S_{\text{xq}} \): Diện tích xung quanh hình nón.
• \( r \): Bán kính đáy hình nón.
• \( l \): Đường sinh của hình nón.

Ví dụ: Một hình nón có bán kính đáy \( r = 5 \) cm và đường sinh \( l = 13 \) cm. Tính diện tích xung quanh của hình nón.

Lời giải

Áp dụng công thức:

$ S_{\text{xq}} = \pi r l = \pi \cdot 5 \cdot 13 = 65\pi \ \text{(cm}^2\text{)}. $

2. Tính diện tích toàn phần của hình nón

Công thức: $ S_{\text{tp}} = S_{\text{xq}} + S_{\text{đáy}} = \pi r l + \pi r^2 = \pi r (l + r). $

Trong đó:

• \( S_{\text{tp}} \): Diện tích toàn phần.
• \( S_{\text{xq}} \): Diện tích xung quanh.
• \( S_{\text{đáy}} = \pi r^2 \): Diện tích đáy.

Ví dụ: Một hình nón có bán kính đáy \( r = 6 \) cm và đường sinh \( l = 10 \) cm. Tính diện tích toàn phần.

Lời giải

Áp dụng công thức:

$ S_{\text{tp}} = \pi r (l + r) = \pi \cdot 6 \cdot (10 + 6) = 96\pi \ \text{(cm}^2\text{)}. $

3. Tính thể tích của hình nón

Công thức: $ V = \frac{1}{3} \pi r^2 h $

Trong đó:

• \( V \): Thể tích hình nón.
• \( r \): Bán kính đáy.
• \( h \): Chiều cao của hình nón.

Ví dụ: Một hình nón có bán kính đáy \( r = 4 \) cm và chiều cao \( h = 9 \) cm. Tính thể tích của hình nón.

Lời giải

Áp dụng công thức:

$ V = \frac{1}{3} \pi r^2 h = \frac{1}{3} \pi \cdot 4^2 \cdot 9 = 48\pi \ \text{(cm}^3\text{)}. $

4. Tính các yếu tố của hình nón khi biết một số thông tin

Tính đường sinh \( l \)

Công thức: Từ định lý Pythagoras: $ l = \sqrt{r^2 + h^2} $

Trong đó:

• \( l \): Đường sinh.
• \( r \): Bán kính đáy.
• \( h \): Chiều cao.

Ví dụ: Một hình nón có bán kính đáy \( r = 6 \) cm và chiều cao \( h = 8 \) cm. Tính đường sinh \( l \).

Lời giải

Áp dụng công thức: $ l = \sqrt{r^2 + h^2} = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = 10 \ \text{cm}. $

Tính bán kính \( r \)

Công thức: Từ định lý Pythagoras: $ r = \sqrt{l^2 – h^2}. $

Ví dụ: Một hình nón có đường sinh \( l = 13 \) cm và chiều cao \( h = 12 \) cm. Tính bán kính đáy \( r \).

Lời giải

Áp dụng công thức:

$r = \sqrt{l^2 – h^2} = \sqrt{13^2 – 12^2} = \sqrt{169 – 144} = 5 \ \text{cm}.$

Tính chiều cao \( h \)

Công thức: Từ định lý Pythagoras: $h = \sqrt{l^2 – r^2}.$

Ví dụ: Một hình nón có đường sinh \( l = 10 \) cm và bán kính đáy \( r = 6 \) cm. Tính chiều cao \( h \).

Lời giải

Áp dụng công thức:

$h = \sqrt{l^2 – r^2} = \sqrt{10^2 – 6^2} = \sqrt{100 – 36} = 8 \ \text{cm}.$

Khi một hình nón bị cắt bởi một mặt phẳng song song với đáy, ta được một hình nón cụt.

Công thức tính diện tích xung quanh hình nón cụt, diện tích toàn phần hình nón cụt, thể tích hình nón cụt

5. Bài tập vận dụng

Bài tập 1.Thả 10 chiếc đinh có kích thước như Hình 9.31 vào một cốc nước thuỷ tinh. Đinh chìm hẳn xuống và nước trong cốc không bị trần ra ngoài. Hỏi thể tích nước trong cốc tăng thêm bao nhiêu mililit (làm tròn kết quả đến hàng phần mười)?

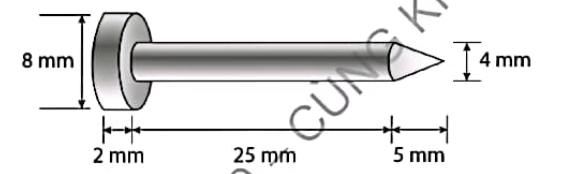
Lời giải

Thể tích phần chân đinh hình trụ:

\(V = \pi {r^2}h = \pi {.4^2}.2 = 32\pi \) mm³

Thể tích phần thân đinh hình trụ:

\(V = \pi {r^2}h = \pi {.2^2}.25 = 100\pi \) mm³

Thể tích phần hình nón:

\(V = \frac{1}{3}\pi {r^2}h = \frac{1}{3}.\pi {.2^2}.5 = \frac{{20}}{3}\pi \) mm³

Thể tích nước tăng thêm là:

\(10.\left( {32\pi  + 100\pi  + \frac{{20}}{3}\pi } \right) \approx 4356,3\) mm³.

Bài tập 2. Tính diện tích bìa cần dùng (theo centimet vuông) để làm một chiếc mũ sinh nhật có dạng hình nón như Hình 9.30 với đường kính đáy 22 cm và chiều cao 18 cm (bỏ qua các mép nối và phần thừa, làm tròn kết quả đến centimet vuông).

Lời giải

Bán kính đáy mũ sinh nhật là:

\(\frac{{22}}{2} = 11\) cm

Đường sinh của mũ sinh nhật là:

\(\sqrt {{{11}^2} + {{18}^2}}  \approx 21\) cm

Diện tích xung quanh của hình nón:

\({S_{xq}} = \pi rn = \pi .11.21 \approx 725\) cm².

Bài tập 3. Phần mái lá của một ngôi nhà có dạng hình nón (không có đáy) với đường kính đáy khoảng 12 m và độ dài đường sinh khoảng 8,5 m (Hình 26). Chi phí để làm phần mái lá đó là 250 000 đồng/1 \(m^2\). Hỏi tổng chi phí để làm toàn bộ phần mái nhà đó là bao nhiêu đồng?

Lời giải

Phần mái lá của một ngôi nhà được biểu diễn dạng hình học như hình sau:

Bán kính đáy là: \(12:2 = 6\left( m \right).\)

Diện tích xung quanh của mái lá là:

\({S_{xq}} = \pi rl = \pi .6.8,5 \approx 160,14\left( {{m^2}} \right).\)

Tổng chi phí để làm toàn bộ phần mái nhà đó là:

\(160,14.250000 = 40.035.000\)(đồng).

Vậy tổng chi phí để làm toàn bộ phần mái nhà đó là \(40.035.000\) đồng.

Bài tập 4. Tính thể tích của hình nón biết:

a) Bán kính đáy 6 cm, chiều cao 12 cm;

b) Đường kính của mặt đáy là 7 m, chiều cao 10 m;

c) Diện tích đáy 152 cm², chiều cao 6 cm;

d) Chu vi đáy 130 cm, chiều cao 24 cm.

Lời giải

a) Thể tích hình nón là: \(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.6^2}.12 = 144\pi \) (cm³).

b) Bán kính đáy là: \(r = \frac{d}{2} = \frac{7}{2}\) = 3,5 (m).

Thể tích hình nón là: \(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .3,{5^2}.10 =\frac{245}{6}\pi \) (m³).

c) Bán kính đáy \(r = \sqrt {\frac{{{S_{đáy}}}}{\pi }}  = \sqrt {\frac{{152}}{\pi }}\)cm

Thể tích hình nón là:

\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi {.\sqrt {\frac{{152}}{\pi }}^2}.6 = 304\) (cm³).

d) Bán kính đáy là: \(r = \frac{{130}}{{2\pi }} = \frac{{65}}{\pi }\) (cm).

Thể tích hình nón là:

\(V = \frac{1}{3}Sh = \frac{1}{3}\pi {r^2}h = \frac{1}{3}\pi .{\left( {\frac{{65}}{\pi }} \right)^2}.24 = \frac{{33800}}{\pi }\) (cm³).

Bài tập 5. Một cái mũ chú hề có kích thước như Hình 13. Hãy tính tổng diện tích giấy làm nên chiếc mũ (không tính phần hao hụt, kết quả làm tròn đến hàng đơn vị).

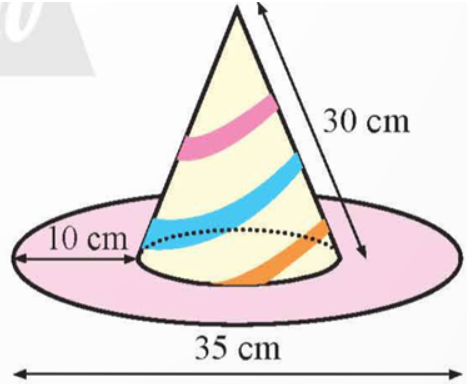
Lời giải

Diện tích phần làm nón là:

\({S_{xq}} = \pi rl = \pi .\left( {\frac{{35}}{2} – 10} \right).30 = 225\pi \) (cm²).

Diện tích phần làm vành mũ là:

\({S_{vanh}} = \pi {\left( {\frac{{35}}{2}} \right)^2} – \pi .{\left( {\frac{{35}}{2} – 10} \right)^2} = 250\pi \) (cm²).

Tổng diện tích để làm mũ là:

\({S_{xq}} + \) \({S_{vanh}} = 225\pi  + 250\pi  \approx \)1492 (cm²).

Bài 6 (Đề thi thử THCS Xuân Giang, 24 – 6 – 2020)

Bác An có một ống đồng cắt hình nón cao 2 m, đường kính đáy 6 m; bác tính ráng đổ sàu xong thì cát rớt xuống lấp một diện tích 30 m² cát. Bác An cần mua bao nhiêu mét khối (m³) cát nữa để lấp đầy hố? (Lấy \( \pi = 3,14 \) và các kết quả gần tròn đến chữ số thập phân thứ hai).

Giải

Vì ống cắt nón có chiều cao \( h = 2 \) m và bán kính đáy \( R = \frac{6}{2} = 3 \) m, nên thể tích cát cần lấp đầy là:

$ V_{\text{đống cát}} = \frac{1}{3} \pi R^2 h = \frac{1}{3} \times 3,14 \times 3^2 \times 2 $

$ = \frac{1}{3} \times 3,14 \times 9 \times 2 = 18,84 \text{ m}^3 $

Bác An cần mua thêm: $30 – 18,84 = 11,16 \text{ m}^3$

Vậy bác An cần mua 11,16 m³ cát bổ sung.

.
Các bài toán liên quan đến hình nón rất đa dạng, bao gồm diện tích, thể tích, các yếu tố liên quan đến đường sinh, bán kính, chiều cao, và các bài toán thực tế như tính thể tích chất lỏng hoặc cắt hình nón. Nắm vững các công thức và kỹ năng tư duy hình học sẽ giúp giải quyết tốt các bài toán liên quan đến hình nón trong học tập và thực tế.