Ở bài công thức Toán hình lớp 9, HinhHoc đã giới thiếu sơ lược về các công thức thường gặp ở hình trụ. Dưới đây là các dạng bài tập phổ biến về hình cầu cùng với công thức áp dụng:
Hình trụ là một khối hình học ba chiều có hai đáy là hai hình tròn bằng nhau và song song với nhau.
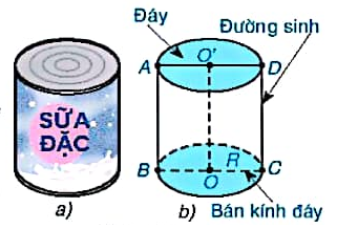
Nó được mô tả bằng ba yếu tố chính: bán kính đáy (R), chiều cao (h) và đường kính đáy (d = 2R).

1. Công thức tính diện tích và thể tích hình trụ
Có 3 công thức thường gặp:
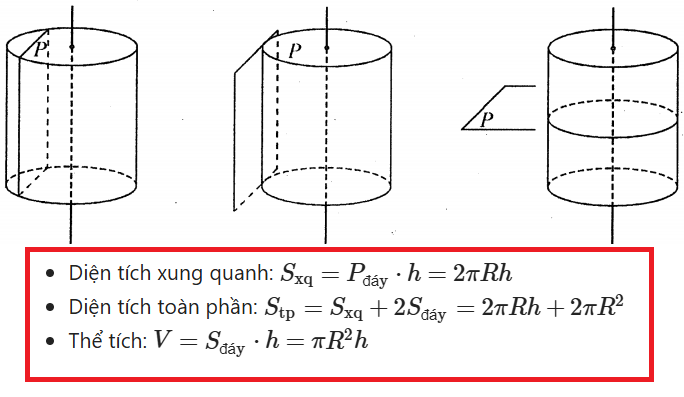
- Diện tích xung quanh: \( S_{xq} = 2 \pi r h \) với r: bán kính đáy, h: chiều cao hình trụ)
- Diện tích toàn phần: \( S_{tp} = 2 \pi r h + 2 \pi r^2 = 2 \pi r (r + h) \)
- Thể tích: \( V = \pi r^2 h \)
Ví dụ 1: Cho hình trụ có bán kính đáy \( r = 5 \, \text{cm} \) và chiều cao \( h = 10 \, \text{cm} \). Tính:
a) Diện tích xung quanh.
b) Diện tích toàn phần.
c) Thể tích.
Lời giải
a) Công thức tính diện tích xung quanh hình trụ:
\( S_{xq} = 2 \pi r h = 2 \pi \cdot 5 \cdot 10 = 100 \pi \, \text{cm}^2 \).
\( S_{xq} = 314 \, \text{cm}^2 \), nếu lấy \( \pi = 3,14 \)
b) Công thức tính diện tích toàn phần hình trụ:
\( S_{tp} = 2 \pi r h + 2 \pi r^2 = 100 \pi + 50 \pi = 150 \pi \, \text{cm}^2 \).
Kết quả: \( S_{tp} = 471 \, \text{cm}^2 \), nếu lấy \( \pi = 3,14 \)
c) Công thức thể tích của hình trụ:
\( V = \pi r^2 h = \pi \cdot 5^2 \cdot 10 = 250 \pi \, \text{cm}^3 \).
Kết quả: \( V = 785 \, \text{cm}^3 \)
2. Cắt hình trụ bởi mặt phẳng
Dạng 1: Thiết diện vuông góc với trục
– Khi cắt hình trụ bằng mặt phẳng vuông góc với trục, thiết diện là một hình tròn.
Diện tích thiết diện: \( S = \pi r^2 \).
Dạng 2: Thiết diện song song với trục
Khi cắt hình trụ bằng mặt phẳng song song với trục, thiết diện là một hình chữ nhật.
Diện tích thiết diện: \( S = 2r \cdot h \), với \( 2r \) là đường kính đáy hình trụ.
Ví dụ: Cho hình trụ có bán kính đáy \( r = 4 \, \text{cm} \) và chiều cao \( h = 6 \, \text{cm} \).
a) Tính diện tích thiết diện khi cắt vuông góc với trục.
b) Tính diện tích thiết diện khi cắt song song với trục.
Lời giải
a) Thiết diện vuông góc với trục:
Diện tích thiết diện là diện tích hình tròn: \( S = \pi r^2 = \pi \cdot 4^2 = 16 \pi \, \text{cm}^2 \).
Kết quả: \( S = 50,24 \, \text{cm}^2 \), nếu lấy \( \pi = 3,14 \)
b) Thiết diện song song với trục:
Thiết diện là hình chữ nhật có chiều dài \( 2r = 8 \, \text{cm} \) và chiều rộng \( h = 6 \, \text{cm} \).
\( S = 2r \cdot h = 8 \cdot 6 = 48 \, \text{cm}^2 \).
Kết quả: \( S = 48 \, \text{cm}^2 \)
3. Hình chữ nhật quay quanh trục để tạo thành hình trụ
Một hình chữ nhật có chiều dài \( a \) và chiều rộng \( b \) quay quanh một cạnh cố định để tạo thành hình trụ.
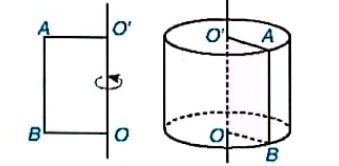
- Bán kính đáy hình trụ: \( r = b \) (cạnh vuông góc với trục).
- Chiều cao hình trụ: \( h = a \) (cạnh dọc theo trục).
- Thể tích hình trụ: \( V = \pi r^2 h = \pi b^2 a \).
- Diện tích toàn phần: \( S_{tp} = 2 \pi r (r + h) \).
Ví dụ: Cho hình chữ nhật có chiều dài \( 12 \, \text{cm} \) và chiều rộng \( 5 \, \text{cm} \). Quay hình chữ nhật quanh cạnh dài để tạo ra hình trụ. Tính:
a) Bán kính đáy và chiều cao hình trụ.
b) Thể tích và diện tích toàn phần của hình trụ.
Lời giải
a) Bán kính đáy và chiều cao:
- Bán kính đáy: \( r = 5 \, \text{cm} \).
- Chiều cao: \( h = 12 \, \text{cm} \).
b) Thể tích:
\( V = \pi r^2 h = \pi \cdot 5^2 \cdot 12 = 300 \pi \, \text{cm}^3 \).
c) Diện tích toàn phần:
${S_{tp}} = 2\pi r(r + h)$
$ = 2\pi \cdot 5 \cdot (5 + 12)$
$ = 2\pi \cdot 5 \cdot 17$
$ = 170\pi {\mkern 1mu} {\kern 1pt} \left( {{\rm{c}}{{\rm{m}}^2}} \right)$
4. Thể tích hình trụ ngoại tiếp hoặc nội tiếp hình cầu
Hình trụ nội tiếp hình cầu:
- Bán kính đáy hình trụ: \( r = \sqrt{R^2 – (h/2)^2} \).
- Thể tích: \( V = \pi r^2 h \).
Hình trụ ngoại tiếp hình cầu:
- Bán kính đáy hình trụ: \( r = R \).
- Chiều cao: \( h = 2R \).
- Thể tích: \( V = \pi R^2 \cdot 2R = 2 \pi R^3 \).
Ví dụ: Cho hình cầu có bán kính \( R = 7 \, \text{cm} \). Một hình trụ nội tiếp hình cầu có chiều cao bằng \( 10 \, \text{cm} \). Tính thể tích của hình trụ.
Lời giải
Bán kính đáy hình trụ:
$r = \sqrt {{R^2} – {{\left( {\frac{h}{2}} \right)}^2}} $
$ = \sqrt {{7^2} – {{\left( {\frac{{10}}{2}} \right)}^2}} $
$ = \sqrt {49 – 25} $
$ = \sqrt {24} $
$ = 4,9{\mkern 1mu} {\kern 1pt} \left( {{\rm{cm}}} \right)$
Thể tích hình trụ:
$V = \pi {r^2}h$
$ = \pi \cdot {(4,9)^2} \cdot 10$
$ = \pi \cdot 24,01 \cdot 10$
$ = 240,1\pi {\mkern 1mu} {\kern 1pt} \left( {{\rm{c}}{{\rm{m}}^3}} \right)$
5. Bài tập vận dụng
Bài 1 (Đề thi TS vào 10 của Hà Nội, năm học 2019 – 2020)
Một bồn nước inox có dạng hình trụ với chiều cao 1,75 m và diện tích đáy là 0,32 m². Hỏi bồn nước này đựng được bao nhiêu mét khối nước? (Bỏ qua bề dày của bồn).
Giải
Vì bồn nước hình trụ có chiều cao \( h = 1,75 \) m và diện tích đáy \( S_{\text{đáy}} = 0,32 \) m², nên thể tích của bồn là:
$V_{\text{bồn}} = S_{\text{đáy}} \times h = 0,32 \times 1,75 = 0,56 \text{ m}^3$
Vậy bồn đựng được 0,56 m³ nước.
Note: Thể tích nước = Thể tích bồn
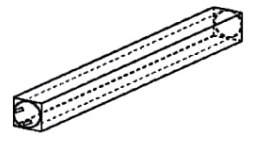
Bài 2. Một bóng đèn huỳnh quang có dạng hình trụ được đặt khít vào một hộp giấy cứng dạng hình hộp chữ nhật (H.10.15). Hộp giấy có chiều dài bằng 0,6m, đáy là hình vuông cạnh 4cm. Tính diện tích xung quanh và thể tích của bóng đèn (giả sử bề dày của hộp giấy không đáng kể).
Lời giải
Bóng đèn huỳnh quang đó có chiều cao bằng \(h = 0,6m = 60cm\) và đường kính đáy 4cm nên bán kính đáy là \(R = 2cm\).
Diện tích xung quanh của bóng đèn là:
\({S_{xq}} = 2\pi Rh = 2\pi .60.2 = 240\pi \left( {c{m^2}} \right)\).
Thể tích của bóng đèn là:
V = Sđáy.h\( = \pi {R^2}h\)\( = \pi {.2^2}.60 = 240\pi \left( {c{m^3}} \right)\).
Bài 3. Phần bên trong một chiếc thùng có dạng hình trụ với bán kính đáy 0,6 m , chiều cao 0,8 m. Người ta muốn sơn mặt bên trong hình trụ (bao gồm mặt đáy). Hỏi diện tích cần sơn là bao nhiêu (kết quả làm tròn đến hàng phần trăm).
Lời giải
Diện tích cần sơn là:
\({S_{tp}} = {S_{xq}} + {S_{đáy}} = 2\pi rh + \pi {r^2} = 2\pi .0,6.0.8 + \pi .0,{6^2} \approx 4,15 (m^2)\)
Bài 4. Phần bên trong của một cái bể hình trụ có chiều cao 2,1 m và bán kính đáy 1,5 m. Tính thể tích lượng nước trong bể biết mực nước bằng \(\frac{2}{3}\)chiều cao của bể (kết quả làm tròn đến hàng đơn vị).
Lời giải
Thể tích của bể là: V = \(\pi \)r2h = \(\pi \).1,52.2,1 = 4,725\(\pi \) (m3).
Thể tích lượng nước trong bể là:
\(V’ = \frac{2}{3}V = \frac{2}{3}.4,725\pi \approx\) 10 (m3).
Bài 5. Một doanh nghiệp sản xuất vỏ hộp bằng tôn có dạng hình trụ với hai đáy (Hình 13). Hình trụ đó có đường kính đáy khoảng 57 cm và chiều cao khoảng 89 cm. Chi phí để sản xuất vỏ hộp đó là 100 000 đồng/m2. Hỏi số tiền mà doanh nghiệp cần chi để sản suất 1 000 vỏ hộp đó là bao nhiêu đồng (làm tròn kết quả đến hàng nghìn).
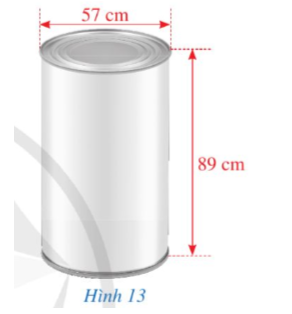
Lời giải
Diện tích toàn phần của vỏ hộp là
\({S_{tp}} = 2\pi rh + 2\pi {r^2}\)
\(= 2\pi .\frac{{57}}{2}.89 + 2\pi .{\left( {\frac{{57}}{2}} \right)^2} \)
\(= 6697,5\pi (cm^2) = 0,66975\pi (m^2)\).
Số tiền mà doanh nghiệp cần chi để sản xuất 1000 vỏ hộp đó là:
\(0,66975\pi.1000.100000 = 66975000\pi \approx 210\,302\,000\) (đồng).
Bài 6. Pin là nguồn năng lượng phổ biến được sử dụng trong nhiều dụng cụ và thiết bị trong gia đình. Pin AAA (hay pin 3A) là một loại pin khô, thường được dùng trong những thiết bị điện tử cầm tay, chẳng hạn, điều khiển từ xa ti vi, máy nghe nhạc MP3, … Mỗi chiếc pin 3A có dạng hình trụ (Hình 15), với kích cỡ tiêu chuẩn: chiều cao khoảng 44,5 mm và đường kính đáy khoảng 10,5 mm. Tính diện tích xung quanh, diện tích toàn phần (theo đơn vị centimét vuông) và thể tích (theo đơn vị centimét khối) của một chiếc pin 3A đó (làm tròn kết quả đến hàng phần mười).

Lời giải
Bán kính đáy là: \(10,5:2 = 5,25\left( {mm} \right).\)
Diện tích xung quanh của cục pin là:
\(2\pi .r.h \approx 2.3,14.5,25.44,5 = 1467,165\left( {m{m^2}} \right) \approx 14,7\left( {c{m^2}} \right).\)
Diện tích toàn phần của cục pin là:
\(2\pi .r.h + 2.\pi .{r^2} \approx 2.3,14.5,25.44,5 + 2.3,14.5,{25^2}\)
\(= 1640,2575\left( {m{m^2}} \right) \approx 16,4\left( {c{m^2}} \right)\)
Thể tích của cục pin là:
\(S.h = \pi .{r^2}h \approx 3,14.5,{25^2}.44,5 \approx 3851,3\left( {m{m^3}} \right) \approx 3,9\left( {c{m^3}} \right)\)
Bài tập 7. Từ một tấm bìa hình chữ nhật với đồ dài hai cạnh là 20 cm, 15 cm có thể cuộn lại và dùng băng dính dán thành hình trụ A hoặc hình trụ B (không có nắp) như Hình 9.13.
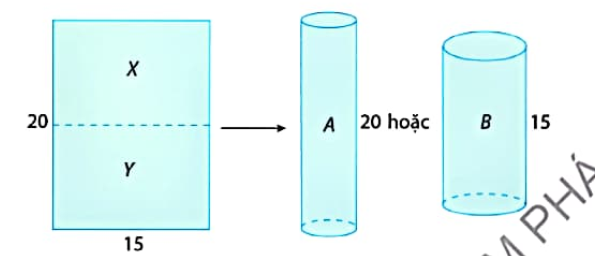
a) Hãy so sánh thể tích của hai hình trụ A và B. Giải thích câu trả lời của em.
b) Nếu cắt tấm bìa thành hai phần X, Y bằng nhau và tạo thành hai hình trụ (không có nắp) cùng chiều cao 15 cm thì tổng thể tích của hai hình trụ này có lớn hơn thể tích của hình trụ B không? Vì sao?
Lời giải
a) Ta có chu vi đường tròn đáy hình trụ A là:
\(2\pi r = 15\)suy ra r = \(\frac{{15}}{{2\pi }}\) cm
Thể tích hình trụ A là:
\({V_A} = \pi {r^2}h = \pi .{\left( {\frac{{15}}{{2\pi }}} \right)^2}.20 = \frac{{1125}}{\pi }\) cm3
Ta có chu vi đường tròn đáy hình trụ B là:
\(2\pi r = 20\)suy ra r = \(\frac{{20}}{{2\pi }} = \frac{{10}}{\pi }\) cm
Thể tích hình trụ B là:
\({V_B} = \pi {r^2}h = \pi .{\left( {\frac{{10}}{\pi }} \right)^2}.15 = \frac{{1500}}{\pi }\) cm3
Vậy thể tích hình trụ B lớn hơn thể tích hình trụ A.
b) Ta có chu vi đường tròn đáy hình trụ chiều cao 15 cm là:
\(2\pi r = 10\)suy ra r = \(\frac{5}{\pi }\) cm
Thể tích hình trụ chiều cao 15 cm là:
\(\pi {r^2}h = \pi .{\left( {\frac{5}{\pi }} \right)^2}.15 = \frac{{375}}{\pi }\) cm3
Suy ra thể tích hai hình trụ chiều cao 15 cm là:
\(\frac{{375}}{\pi }\) = \(\frac{{750}}{\pi }\) cm3
Vậy tổng thể tích của hai hình trụ chiều cao 15 cm nhỏ hơn thể tích của hình trụ B.