Để học tốt hình học 9, bài viết này sẽ giúp bạn tóm tắt các công thức toán hình lớp 9 của 2 học kì 1 và học kì 2 chi tiết nhất theo chương trình sách mới Kết nối tri thức, Chân trời sáng tạo, Cánh diều. Hi vọng loạt bài này sẽ như là cuốn sổ tay công thức giúp bạn học tốt môn Toán lớp 9 hơn.
Công thức toán hình lớp 9: Hình học phẳng
1. Tỉ số lượng giác của góc nhọn
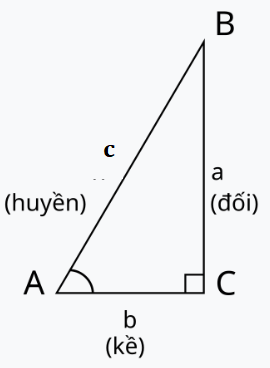
\({\rm{sin\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,huyền}}\)
\({\rm{cos\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,huyền}}\)
\({\rm{tan\alpha }} = \frac{{cạnh\,đối}}{{cạnh\,kề}}\)
\({\rm{cot\alpha }} = \frac{{cạnh\,kề}}{{cạnh\,đối}}.\)
\(\cot \alpha = \frac{1}{{\tan \alpha }}\).
\(\sin \alpha ,\cos \alpha ,\tan \alpha ,\cot \alpha \) gọi là các tỉ số lượng giác của góc nhọn \(\alpha \).
2. Đường tròn và Diện tích hình quạt tròn; hình vành khuyên
Đường tròn tâm O bán kính R (R > 0), kí hiệu là (O; R), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R.
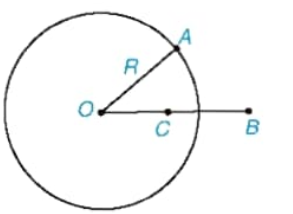
- Đường tròn là hình có tâm đối xứng; tâm của đường tròn là tâm đối xứng của nó. Đường tròn có một tâm đối xứng.
- Đường tròn là hình có trục đối xứng; mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng của nó. Đường tròn có vô số trục đối xứng.
- Mỗi dây đi qua tâm là một đường kính của đường tròn và đường kính là dây cung lớn nhất.
- Góc ở tâm là góc có đỉnh trùng với tâm của đường tròn.
Cung của đường tròn là một phần của đường tròn được giới hạn bởi hai điểm trên đường tròn. Dựa vào độ dài của cung so với chu vi của đường tròn, cung được chia thành hai loại chính:
- Cung nhỏ: Là cung có số đo góc ở tâm nhỏ hơn 180°.
- Cung lớn: Là cung có số đo góc ở tâm lớn hơn 180°.
- Cung nửa đường tròn: Khi hai điểm tạo thành cung đối diện nhau trên đường tròn, cung đó chính là nửa đường tròn, có số đo góc ở tâm bằng 180°.
Công thức quan trọng:
- Chu vi: \(C = \pi d = 2\pi R\)
- Công thức tính độ dài l của cung tròn \({n^o}\) trên đường tròn (O;R) là: \(l = \frac{n}{{180}}\pi R\)
- Hình quạt tròn là phần hình tròn giới hạn bởi một cung tròn và hai bán kính đi qua hai đầu mút của cung đó và Diện tích \({S_q}\) của hình quạt tròn bán kính R ứng với cung \({n^o}\): \({S_q} = \frac{n}{{360}}\pi {R^2} = \frac{{l.R}}{2}\)
- Hình vành khuyên (còn gọi là hình vành khăn) là phần nằm giữa hai đường tròn có cùng tâm và bán kính khác nhau (còn gọi là hai đường tròn đồng tâm) và Diện tích \({S_v}\) của hình vành khuyên tạo bởi hai đường tròn đồng tâm và có bán kính R và r: \({S_v} = \pi \left( {{R^2} – {r^2}} \right)\) (với R > r)
3. Vị trí tương đối của đường thẳng và đường tròn
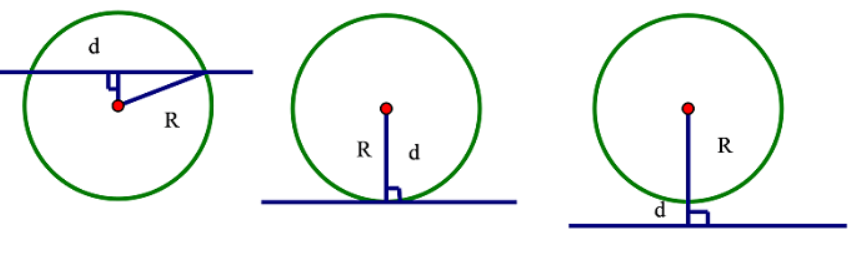
| Vị trí tương đối của đường thẳng và đường tròn | Số điểm chung | Hệ thức giữa d và R |
| Đường thẳng và đường tròn cắt nhau | 2 | d < R |
| Đường thẳng và đường tròn tiếp xúc nhau | 1 | d = R |
| Đường thẳng và đường tròn không giao nhau | 0 | d > R |
4. Vị trí tương đối của hai đường tròn
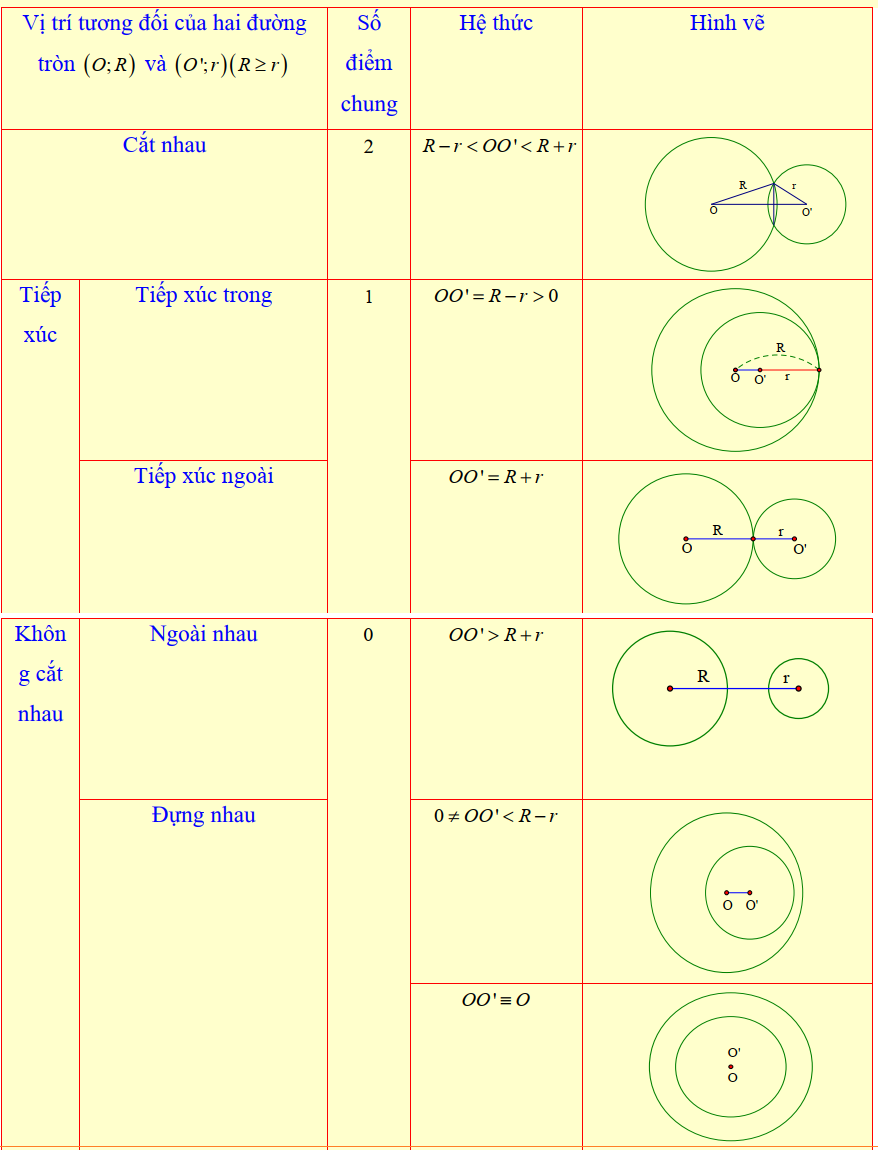
5. Góc nội tiếp
Góc nội tiếp là góc có đỉnh nằm trên đường tròn và hai cạnh chứa hai dây cung của đường tròn đó.
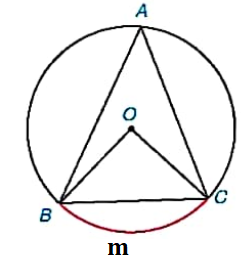
- Góc BAC là góc nội tiếp của đường tròn (O); và nó chắn cung $\overset\frown{BmC}$.
- \(\widehat {BAC} = \frac{1}{2}\)sđ$\overset\frown{BmC}=\frac{1}{2}\widehat{BOC}$.
6. Đường tròn ngoại tiếp và đường tròn nội tiếp của một tam giác
Đường tròn ngoại tiếp của một tam giác là đường tròn đi qua ba đỉnh của tam giác đó.
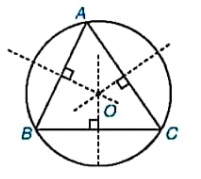
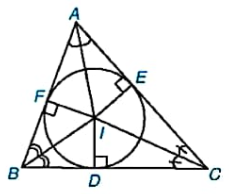
Đường tròn tiếp xúc với ba cạnh của tam giác được gọi là đường tròn nội tiếp tam giác. Tam giác đó được gọi là ngoại tiếp đường tròn. Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác của tam giác.
7. Tứ giác nội tiếp
Tứ giác có bốn đỉnh nằm trên một đường tròn được gọi là tứ giác nội tiếp đường tròn (hoặc đơn giản là tứ giác nội tiếp) và đường tròn được gọi là đường tròn ngoại tiếp tứ giác.
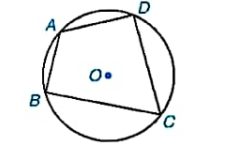
Trong một tứ giác nội tiếp đường tròn, tổng số đo hai góc đối bằng \(180^\circ \).
8. Đa giác đều
Đa giác đều là một đa giác lồi có các cạnh bằng nhau và các góc bằng nhau.

Công thức toán hình lớp 9: Hình học không gian
1. Hình trụ
Nếu Hình trụ có bán kính đáy \( R \) và chiều cao \( h \) thì:
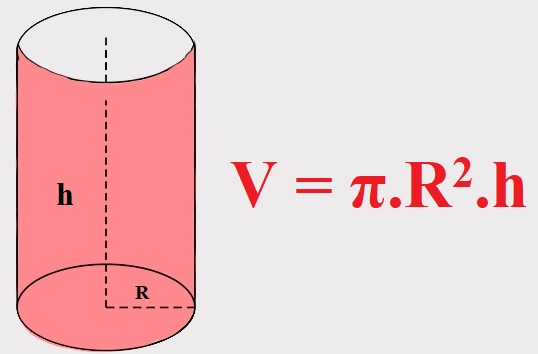
- Diện tích xung quanh: $ S_{\text{xq}} = P_{\text{đáy}} \cdot h = 2\pi R h $
- Diện tích toàn phần: $ S_{\text{tp}} = S_{\text{xq}} + 2S_{\text{đáy}} = 2\pi R h + 2\pi R^2 $
- Thể tích: $ V = S_{\text{đáy}} \cdot h = \pi R^2 h $
Hình trụ là gì? Công thức tính diện tích và thể tích hình trụ
2. Hình cầu
Nếu Hình cầu có bán kính \( R \) thì:
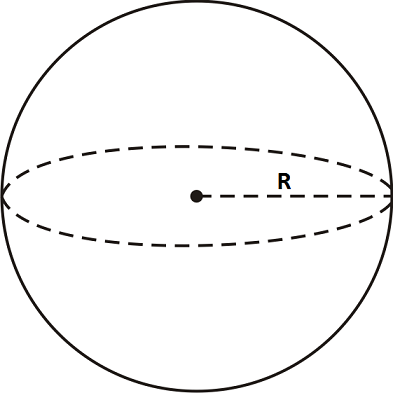
- Diện tích mặt cầu: $ S = 4\pi R^2 $
- Thể tích: $ V = \frac{4}{3} \pi R^3 $
3. Hình nón
Nếu Hình nón có bán kính đáy \( R \), chiều cao \( h \) và đường sinh \( l \) thì:
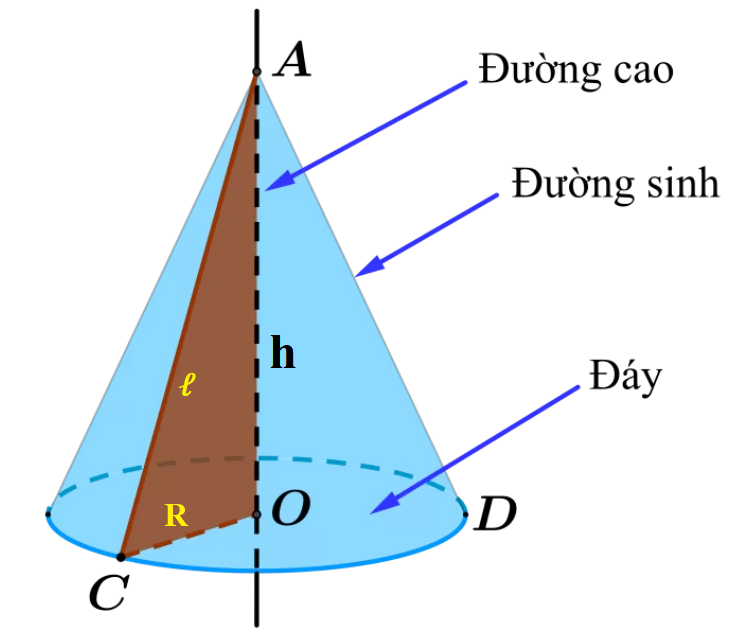
- Diện tích xung quanh: $ S_{\text{xq}} = \pi R l $
- Diện tích toàn phần: $ S_{\text{tp}} = S_{\text{xq}} + S_{\text{đáy}} = \pi R l + \pi R^2 $
- Thể tích: $ V = \frac{1}{3} V_{\text{tru}} = \frac{1}{3} \pi R^2 h $
Hình nón là gì? Công thức tính diện tích xung quanh hình nón và thể tích hình nón
4. Hình nón cụt
Nếu Hình nón cụt có bán kính đáy lớn \( R \), bán kính đáy nhỏ \( r \), chiều cao \( h \) và đường sinh \( l \) thì:
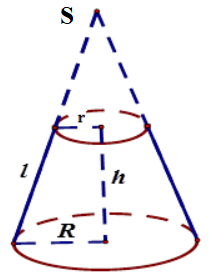
- Diện tích xung quanh: $ S_{\text{xq}} = \pi (R + r) l $
- Diện tích toàn phần: $ S_{\text{tp}} = S_{\text{xq}} + S_{\text{đáy lớn}} + S_{\text{đáy nhỏ}} $ $ = \pi (R + r) l + \pi R^2 + \pi r^2 $
- Thể tích: $ V = \frac{1}{3} \pi (R^2 + r^2 + Rr) h $
