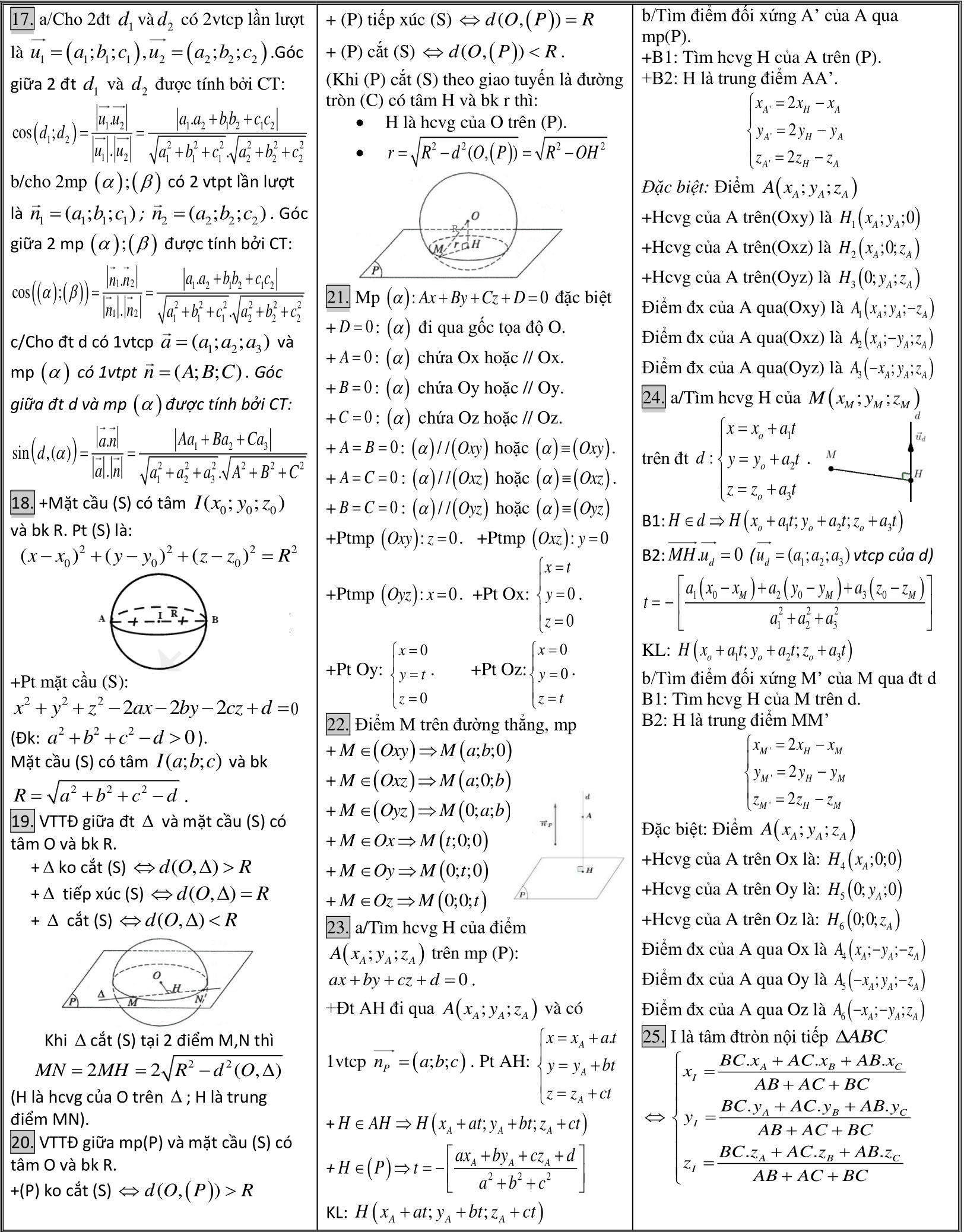
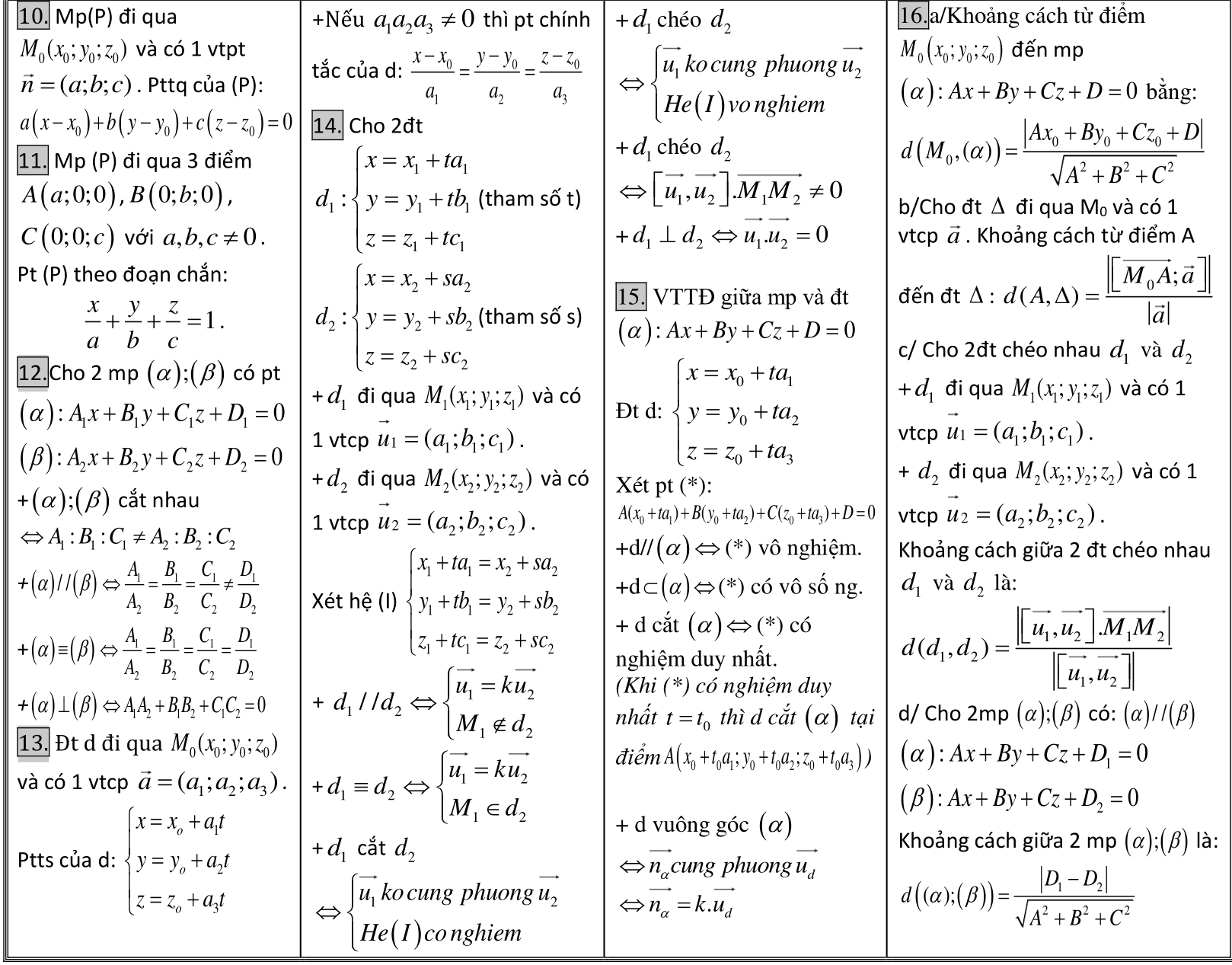
Công thức hình học lớp 12 – “công cụ bí mật” để chinh phục hình học không gian, từ bài tập đơn giản tới các bài phức tạp. Bạn cần nắm chắc lý thuyết, giải bài tập hình học lớp 12 hiệu quả, hay luyện tập công thức để tự tin thi cử? Bài viết này sẽ giúp bạn làm chủ mọi thứ, ngắn gọn và dễ hiểu!
1. Các công thức Toán hình lớp 12 hk1
1.1 Vectơ trong không gian
Tổng của 2 vecto
Phép cộng vectơ trong không gian cũng có các tính chất như phép cộng vectơ trong mặt phẳng
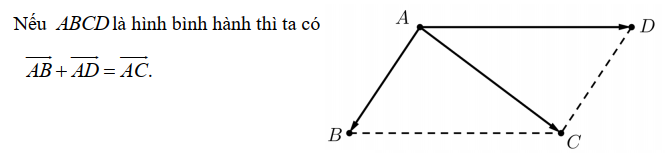
Quy tắc lấy hiệu
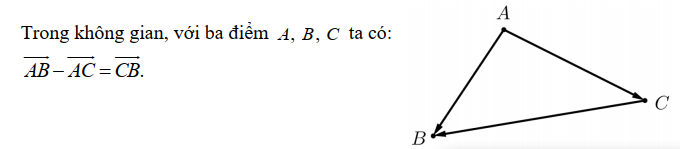
Tích vô hướng của hai vecto trong không gian
Tích vô hướng của hai vecto \(\mathop a\limits^ \to \) và \(\mathop b\limits^ \to \) là một số, được xác định bởi công thức \(\overrightarrow a \cdot \overrightarrow b = \left| {\overrightarrow a } \right| \cdot \left| {\overrightarrow b } \right| \cdot \cos \left( {\overrightarrow a ,\overrightarrow b } \right)\)
1.2 Hệ trục tọa độ trong không gian
Trong không gian Oxyz
- Tọa độ điểm: \(\overrightarrow {OM} = x\overrightarrow i + y\overrightarrow j + z\overrightarrow k \) được gọi là tọa độ của điểm M đối với hệ tọa độ Oxyz. Khi đó, ta viết M = (x,y,z), trong đó x là hoành độ, y là tung độ và z là cao độ của M
- Tọa độ vecto: cho hai điểm \(M({x_M};{y_M};{z_M})\) và \(N({x_N};{y_N};{z_N})\). Khi đó: \(\overrightarrow {MN} = ({x_N} – {x_M};{y_N} – {y_M};{z_N} – {z_M})\)
1.3 Biểu thức tọa độ của các phép toán vectơ
Trong không gian Oxyz, cho hai vecto \(\overrightarrow a = (x;y;z)\) và \(\overrightarrow b = (x’;y’;z’)\). Ta có:
- \(\overrightarrow a + \overrightarrow b = (x + x’;y + y’;z + z’)\)
- \(\overrightarrow a – \overrightarrow b = (x – x’;y – y’;z – z’)\)
- \(k\overrightarrow a = (kx;ky;kz)\) với k là một số thực
Trong không gian Oxyz, cho ba điểm không thẳng hàng \(A({x_A};{y_A};{z_A}),B({x_B};{y_B};{z_B}),C({x_C};{y_C};{z_C})\). Khi đó:
- Tọa độ trung điểm của đoạn thẳng AB là $\left( {\frac{{{x_A} + {x_B}}}{2};\frac{{{y_A} + {y_B}}}{2};\frac{{{z_A} + {z_B}}}{2}} \right)$
- Tọa độ trọng tâm tam giác ABC là $\left( {\frac{{{x_A} + {x_B} + {x_C}}}{3};\frac{{{y_A} + {y_B} + {y_C}}}{3};\frac{{{z_A} + {z_B} + {z_C}}}{3}} \right)$
2. Các công thức Toán hình lớp 12 hk2